[Algorithm] 정렬 알고리즘 & Python3 코드 & 시간복잡도 정리

1. 병합 정렬

분할 정복 방식을 이용한 알고리즘으로 말 그대로 배열을 분할 후 정렬하면서 병합하는 방식이다.

• 배열의 원소를 절반씩 잘라 계속해서 나눈 후 => 분할
• 배열의 원소의 개수가 1개가 되면 이웃한 배열의 원소와 크기를 비교하여 정렬하면서 합치기 => 병합

다음과 같이 그림으로 나타낼 수 있다. 

출처: https://assaeunji.github.io/python/2020-05-06-bj2751/

분할을 하게되면 분할되는 깊이가 N log N에 비례하고 배열을 합치는 과정을 생각하면 최대 배열의 개수는 N개, 즉 원소의 개수만큼 생기게 되어 N에 비례한다. 따라서 병합정렬의 시간 복잡도는 O(N log N) 이다

 

 

Python3 Code

def merge_sort(numbers):
    if len(numbers) <= 1:
        return numbers
    mid = len(numbers)//2
    left = merge_sort(numbers[:mid])
    right = merge_sort(numbers[mid:])

    l, r, i = 0, 0, 0
    while l < len(left) and r < len(right):
        if left[l] >= right[r]:
            numbers[i] = right[r]
            r += 1
        else:
            numbers[i] = left[l]
            l += 1
        i += 1
    if r == len(right):
        while l < len(left):
            numbers[i] = left[l]
            i += 1
            l += 1
    elif l == len(left):
        while r < len(right):
            numbers[i] = right[r]
            i += 1
            r += 1

    return numbers

 

---

시간 복잡도 비교

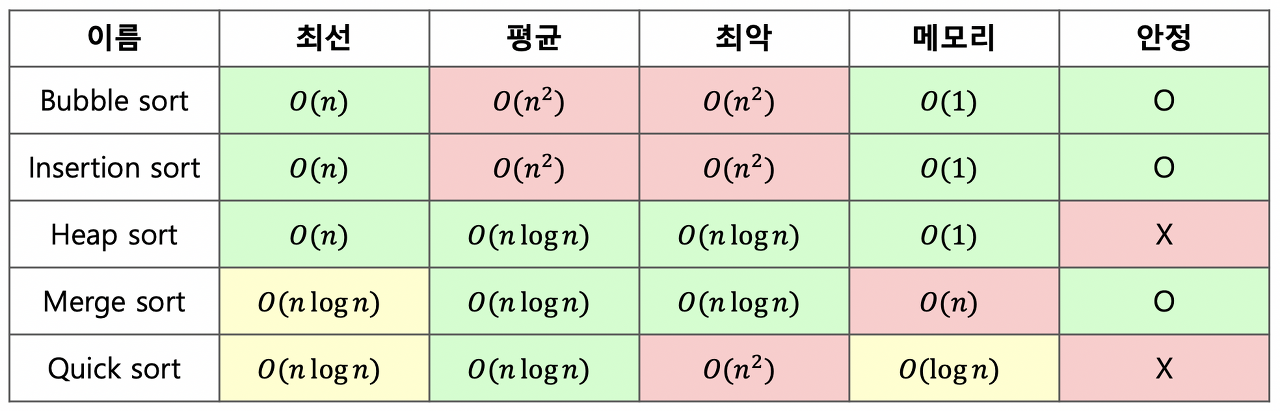
출처 https://d2.naver.com/helloworld/0315536

 

---

참조

:https://assaeunji.github.io/python/2020-05-06-bj2751/

:https://d2.naver.com/helloworld/0315536